动态规划

动态规划的算法核心为明确dp[i]中dp和i代表的含义。

数学方法求解动态规划

96.不同的二叉搜索树

• 题目：给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。
• 解法：找到的DP状态公式：

$$G(n)=\sum_{i=1}^{n}G(i-1)\cdot G(n-i)$$

常规方法可直接根据该状态转移函数求解，现给出数学解法，其中涉及到卡塔兰数：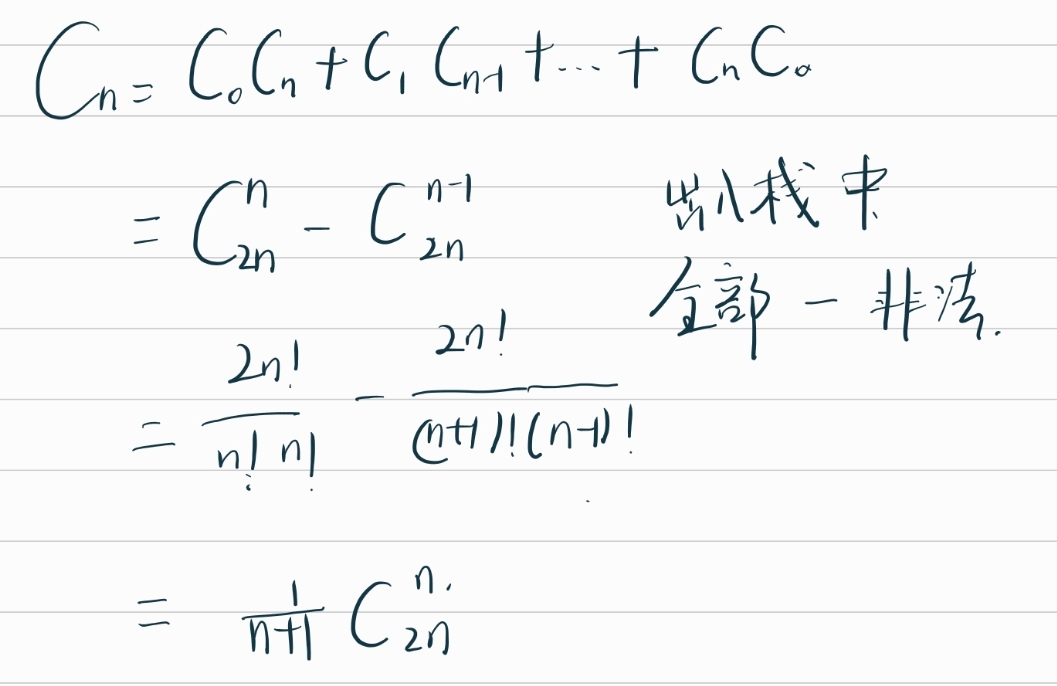

直接根据该组合数求解即可。

背包问题

下面有几种背包的不同问题：

• 取价值最大问题
• 分割等和数组
• 分割最相近数组
• 基于构造目标和组合方案问题
• 基于构造目标和的排列方案问题(甚至是爬楼梯问题)

其中前三种种问题可以归为一类数组求值问题，最后两种可以归为排列组合问题。

这两类不同的问题分别有3个不同之处：

1. dp初始化不同，一个是dp[0]=0一个是dp[0]=1/True，造成这个的原因是dp含义不同，一个代表的是价值，一个代表的是组合数量。
2. 第二层for循环中右侧区间不同，一个是物品的重量一个是物品的序号(对应价值)。
3. dp的状态转移函数不同，一个跟dp[j-i]+i有关，一个跟dp[j-i]有关，原因是dp含义不同。

排列组合问题中求组和要先把遍历物品，求排列要先遍历背包

代码模板

• 0-1背包:
  不同的是单一元素不可重复选取，以下为代码模板：

求值

  dp = [0] * (bagweight+1)
  dp[0] = 0
  for i in values:
      for j in range(bagweight, weight(i)-1, -1 ):
          dp[j] = max(dp[j],dp[j-i]+i)

组合

  dp = [0] * (target+1)
  dp[0] = 1
  for i in nums:
      for j in range(target, i-1, -1 ):
          dp[j] += dp[j-i]

排列

  dp = [0] * (target+1)
  dp[0] = 1  
  for i in range(target, i-1, -1):  
      for j in nums:  
          if i >= j:  
              dp[i] += dp[i - j]

• 完全背包:
  通常应对的是数组元素可放回重复选取的问题。模板如下：

求值

  dp = [0]*(bag_weight+1)
  dp[0] = 0
  for i in range(item_nums):
      for j in range(item_weight[i],bag_weight+1):
          dp[j]=max(dp[j],dp[j-item_weight[i]]+item_values[i])

组合

  dp = [0] * (target+1)
  dp[0] = 1
  for i in nums:
      for j in range(1, target + 1):
          dp[j] += dp[j-i]

排列

  dp = [0] * (target+1)
  dp[0] = 1  
  for i in range(1, target + 1):  
      for j in nums:  
          if i >= j:  
              dp[i] += dp[i - j]

同0-1背包不同的是单一元素可以重复选取，因此循环遍历过程采取正序。

打家劫舍

主要有以下几类问题：

• 普通数组
• 循环数组：分别计算出去第一个和最后一个的普通数组最大值
• 树形结构：后序递归，双参数数组记录
• 值域打家劫舍：相邻多个无法同时打劫

通用转移函数:

# 普通数组
dp[i] = max(dp[i-2]+value(i),dp[i-1])
# 树形数组
return (max(left)+max(right),left[0]+right[0]+root.var)
# 值域打家劫舍
# 需要多加一个判断保证j的范围正确
f[i+1] =max(f[i] , f[j] +value(i+1))

买卖股票

主要有以下几类问题：

• 只能买一次
• 能买无数次
• 只能买k次
• 卖出有冷却期
  解决此类问题通常使用二维数组dp[i][j],其中i代表的是第几天，k代表的是今天的状态(买入，卖出，冷却期)，dp通用模板如下：

  for i in range(1, len(prices)):
      for j in range(1,2*k+1,2):
          dp[i][j]=max(dp[i-1][j],dp[i-1][j-1]-prices[i])
          dp[i][j+1]=max(dp[i-1][j+1],dp[i-1][j]+prices[i])

上面模板针对的是最多买卖k次的情况，若只能买卖1次或无数次dp的列数为2，k次的话则为2k，有冷却期则为3。

数组长度相关

有以下几类为题：

• 最长上升子序列
• 最长连续递增序列
• 最长重复子数组
• 最长公共子序列
• 最短公共超序列
  在这几个问题中动态规划相较于遍历搜索的优势在于，能降低一个维度的时间复杂度，比方说第一个问题最长上升子序列如果使用遍历搜索需要2次方复杂度，动态规划可以降到1次方复杂度。这类问题dp数组代表的含义是相同的，即所求答案的长度。

最长公共子序列
长度n+1，考虑左闭右开。

  if (text1[i - 1] == text2[j - 1]) {
      dp[i][j] = dp[i - 1][j - 1] + 1;
  } else {
      dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
  }

细节：通常设置长度为n+1,考虑所有状态转移过程条件就行，对于可能越界的转移函数就加个if判断。

最短公共超序列

先正向计算出最短超序列长度，再反向填。两字符串最后一个字母相等的话，最短公共超序列最后一个字母肯定也是它们，不等的话就选短的+1.

# 正向计算长度
  if (text1[i - 1] == text2[j - 1]) {
      dp[i][j] = dp[i - 1][j - 1] + 1;
  } else {
      dp[i][j] = min(dp[i - 1][j], dp[i][j - 1])+1;
  }

最长上升子序列：

dp:

for i in range(len(nums)):
  for j in range(i):
      if nums[i] > nums[j]:
          dp[i] = max(dp[i], dp[j] + 1)

二分法：

g = []
for i in range(len(nums)):
  i = bisect_left(g, nums[i])
  if(i==len(g))
    g.append(nums[i])
  else:
    g[i] = nums[i]

最优划分问题
常用dp递推思路类似最长上升子序列。也就是从尾部进行考虑，考虑针对选定的尾，遍历不同的头。

for i in range(len(nums)):
  dp[i] = min(dp[i-1]+1,dp[i])
  for j in range(i):  
    if ....:
      dp[i] = min(dp[i],dp[j]+1)

约束划分问题

考虑的状态转移函数通常是n划分由n-1次划分状态转移而来。

进阶解法

主要针对于dp的优化算法

矩阵快速幂

针对于1维递推表达式如：$dp[i]=dp[i-1]+dp[i-2]$和k维1阶的递推表达式(只与一个相差阶有关系)如：$dp[i][j]=dp[i-1][j-1]+dp[i-1][j-2]$，可以采用矩阵快速幂求解。时间复杂度均为O(logn)快速幂的基本思想如下：

def pow(x,n):
  while n:
    if n&1: 
      res=res*x
    x=x*x
    n>>=1
    return res

递推过程中只需要求出系数矩阵n的幂，即可求出答案。

线段树

线段树是一种树形数据结构，用于存储区间数据，并且支持区间查询。可针对打家劫舍进行优化。且不需要树的数据结构，就用数组以及int就能代替树。
下面是线段树的初始化问题,且假设区间长度为k：

python

# bit_length(k)为k的二进制位数最高位1的位置，相当于log2(k)+1
t = [0 for _ in range(2<<bit_length(k))]]

java

// numberOfLeadingZeros(k)为k的二进制位数前面0的个数，int一共32位，减去前面的0即最前面的1位置
t = new int[2<<(32 - Integer.numberOfLeadingZeros(k))];

下面给出线段树的跌打构造模板：

# 传入的o即为根节。
def build(o,l, r):
  if l==r:
    t[o]=num[l]
  m = (l+r)//2
  build(o*2,l,m)
  build(o*2+1,m+1,r)
  # 融合左右子树，可根据需求调整
  t[o]=t[o*2]+t[o*2+1]