跳至主要內容

SVD分解和PCA主成分析

Lzy2023年9月23日大约 10 分钟机器学习算法svdpca

SVD分解和PCA主成分析

奇异值分解（Singular Value Decomposition，简称SVD）是一种常用的矩阵分解方法，用于将一个矩阵分解为三个矩阵的乘积。SVD在许多领域中都有广泛的应用，如数据降维、图像压缩、推荐系统等。

数学公式表示

SVD的数学公式表示如下：
给定一个 m×nm×n 的矩阵AA，其SVD表示为：

A=UΣVT A = U \Sigma V^T

其中，UU是一个m×mm \times m的酉矩阵，表示AATAA^T的特征向量构成的矩阵；Σ\Sigma是一个m×nm \times n的对角矩阵，表示AA的奇异值构成的矩阵；VV是一个n×nn \times n的酉矩阵，表示ATAA^TA的特征向量构成的矩阵。

几何意义

UU是一个正交矩阵，表示旋转操作；Σ\Sigma是一个对角矩阵，表示缩放操作；VV是另一个正交矩阵，表示再旋转操作。

具体而言，SVD的几何意义可以解释如下：

UU表示将原始空间中的向量旋转到一个新的坐标系中。这个新坐标系的基向量是UU的列向量，它们是原始坐标系中的标准正交基向量的旋转版本。

Σ\Sigma表示在每个坐标轴上的缩放因子。Σ\Sigma的对角线上的元素称为奇异值，它们表示原始向量在每个旋转后的坐标轴上的缩放程度。奇异值按照降序排列，因此，前面的奇异值对应着更重要的特征。

VV表示将旋转后的向量再次旋转回原始坐标系。VV的列向量是原始坐标系中的标准正交基向量的再旋转版本。

总的来说是将一个矩阵通过旋转，拉伸，再旋转，而拉伸即用中间的奇异值矩阵进行表示。通过SVD，我们可以将一个矩阵 AA 表示为一系列几何操作的组合，从而揭示了原始数据的主要几何特征。SVD在降维、信号处理、图像压缩等领域中具有广泛的应用，可以提取数据的重要特征、去除噪声和冗余信息，并帮助理解数据的结构和模式。

SVD算法步骤

SVD算法的基本步骤如下：

  1. 给定一个m×nm \times n的矩阵AA，其中mm是行数，nn是列数。
  2. 计算AA的转置矩阵ATA^T与AA的乘积AATAA^T。
  3. 对AATAA^T进行特征值分解，得到特征值和特征向量。
  4. 计算ATA^T的转置矩阵(AT)T(A^T)^T与ATA^T的乘积ATAA^TA。
  5. 对ATAA^TA进行特征值分解，得到特征值和特征向量。
  6. 根据特征值和特征向量构建奇异值矩阵Σ\Sigma。
  7. 对AA进行奇异值分解，得到矩阵UU、Σ\Sigma和VV。

图像压缩算法实现

这里主要使用python实现对目标图片进行压缩。通过查阅相关资料了解到可以通过使用pytorch中的svd函数进行实现，
也可以通过使用python中numpy库中线性代数相关的函数进行分解，这里选择采用第二种方式。其次这次试验要求
处理的图像为一张图像，因此转化为张量形式之后三维的，通道深度为3，分别表示红绿蓝三色。而传统的SVD分解算法
则只能处理二维矩阵形式，也就是灰度图。因此考虑到两种方法对其进行分解，一种是将3维张量reshape成2维，
在进行相关压缩之后再reshape回来。第二种方法是对3个通道分别进行SVD分解，然后再把三个通道叠加成三维张量
的形式。

方法一

方法一将3维张量reshape成2维，在进行相关压缩之后再reshape回来，并使用pytorch中的SVD函数进行处理。
代码如下：

import numpy as np
import matplotlib.pyplot as plt
import torch

# 读取图片
imag = plt.imread('butterfly.bmp')

tensor_image = torch.tensor(imag)
reshaped_image = tensor_image.reshape(-1,437)
float_image = reshaped_image.float()
U, S, V = torch.svd(float_image)

# 误差
errors=[]

# 按照奇异值数量倒序进行图片展示，每次减少25个奇异值
for k in range(len(S), 0, -25):
# 分解

      compressed_S = np.diag(S[:k])
      compressed_U = U[:, :k]
      compressed_V= V[:k, :]
  
  
      # 计算
      reconstructed_array = np.dot(compressed_U, np.dot(compressed_S, compressed_V))
      
  
      # 回滚
      reconstructed_image_array = reconstructed_array.reshape(imag.shape)
      reconstructed_image = reconstructed_image_array.astype(np.uint8)
      
      # 误差分析
      diff = imag - reconstructed_image
      mse = np.mean(np.square(diff))
      errors.append(mse)
      
      # # 图片展示,如需要可以将注释打开
      # plt.imshow(reconstructed_image)
      # plt.show()

# 误差分析
plt.plot(range(len(S), 0, -25),errors)
plt.xlabel('奇异值数',fontproperties='SimHei')
plt.ylabel('均方误差',fontproperties='SimHei')
plt.show()

下面分别为误差图和压缩图：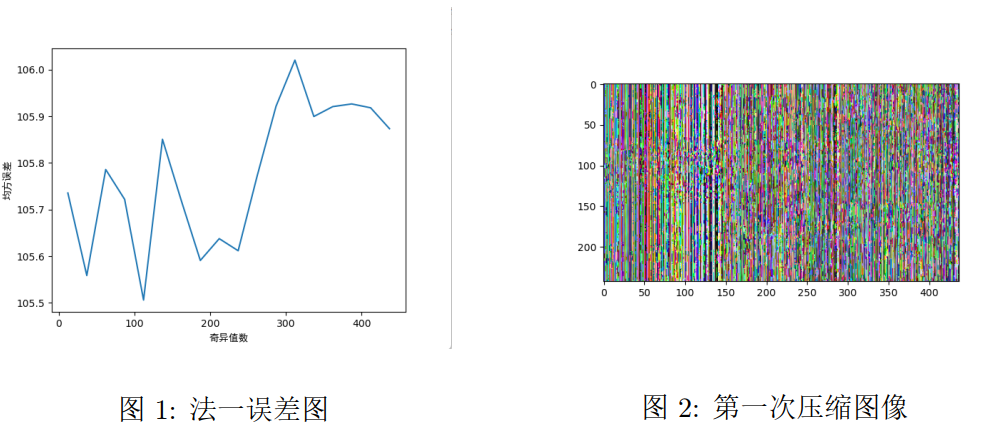
Alt text
可以看到如果先将三维张量压缩为二维在进行SVD分解，之后再还原成三维的方法是不行的。造成这种结果的原因
可能是在将三个通道压缩成一个通道之后，奇异值所代表的特征是三个通道叠加的，在进行相关压缩之后再reshape回来后
就会出现一些错误。

方法二

第二种方法是对3个通道分别进行SVD分解，采用的是numpy库中关于线性代数的相关函数。把三个通道拆分为R，G，B,对三个
不同的矩阵分别处理，之后再叠加，代码如下：

import numpy as np
import matplotlib.pyplot as plt

# 读取图片
imag = plt.imread('butterfly.bmp')

# 图片深度是3，拆分为深度1的3个矩阵分别进行分解
red_channel = imag[:, :, 0]
green_channel = imag[:, :, 1]
blue_channel = imag[:, :, 2]

# 进行分解
U_red, S_red, V_red = np.linalg.svd(red_channel)
U_green, S_green, V_green = np.linalg.svd(green_channel)
U_blue, S_blue, V_blue = np.linalg.svd(blue_channel)

# 误差
errors=[]

# 按照奇异值数量倒序进行图片展示，每次减少25个奇异值
for k in range(len(U_red), 0, -25):
# 分解三个深度
compressed_S_red = np.diag(S_red[:k])
compressed_S_green = np.diag(S_green[:k])
compressed_S_blue = np.diag(S_blue[:k])
# UV分解
compressed_U_red = U_red[:, :k]
compressed_V_red = V_red[:k, :]
compressed_U_green = U_green[:, :k]
compressed_V_green = V_green[:k, :]
compressed_U_blue = U_blue[:, :k]
compressed_V_blue = V_blue[:k, :]
# 计算
compressed_red_channel = np.dot(compressed_U_red, np.dot(compressed_S_red, compressed_V_red))
compressed_green_channel = np.dot(compressed_U_green, np.dot(compressed_S_green, compressed_V_green))
compressed_blue_channel = np.dot(compressed_U_blue, np.dot(compressed_S_blue, compressed_V_blue))
# 合并三个深度
compressed_imag = np.stack([compressed_red_channel, compressed_green_channel, compressed_blue_channel], axis=2)
compressed_imag = compressed_imag.astype(np.uint8)
# 误差分析
diff = imag - compressed_imag
mse = np.mean(np.square(diff))
errors.append(mse)
# # 图片展示,如需要可以将注释打开
# plt.imshow(compressed_imag)
# plt.show()
#误差分析
plt.plot(range(len(U_red), 0, -25),errors)
plt.xlabel('奇异值数',fontproperties='SimHei')
plt.ylabel('均方误差',fontproperties='SimHei')
plt.show()

下面为第二次的误差图：

该误差图是将奇异值从大到小进行排序后，依次减少25个奇异值并分析其误差画出来的
折线图，可以看出在初期减少奇异值的时候误差变化并不大，原因在于刚开始减小的是一些
数值比较小的奇异值，可以解释为这些奇异值对该图像的特征并没什么影响。

下面为第二次压缩图像：

PCA主成分分析

主成分分析（Principal Component Analysis，简称PCA）是一种常用的数据降维和特征提取技术。它通过线性变换将原始数据投影到一个新的坐标系中，使得投影后的数据具有最大的方差。在图片压缩中，PCA可以用于降低图像的维度，从而实现图片的压缩。

数学公式表示

给定一个m×nm \times n的矩阵DD，其PCA表示为：

D=S−1R−1D′            D′=RSD D=S^{-1}R^{-1}D'~~~~~~~~~~~~D'= RSD

其中，D′D'是待分析的矩阵，RR表示对该矩阵进行旋转操作，主要目的是找到数值方差最大的作为主轴，DD是一个对角矩阵
目的是为了对图片进行拉伸操作，DD则为处理过后的矩阵。

几何意义

给定一个包含nn个样本的数据集X=x1,x2,…,xn\mathbf{X}={\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n}，其中每个样本xi\mathbf{x}_i是一个dd维向量。PCA算法的目标是找到一个dd维的正交变换矩阵W\mathbf{W}，将原始数据X\mathbf{X}投影到新的坐标系中，使得投影后的数据具有最大的方差。

图像压缩算法实现

  1. 数据预处理： 首先，将图片转换为灰度图像。如果图片是彩色图像，可以将其转换为灰度图像，这样每个像素只有一个灰度值。然后，将每个像素的灰度值归一化到0到1的范围，以便统一数据的尺度。

  2. 构建数据矩阵： 将归一化后的图片数据转换为一个数据矩阵，其中每一列代表一个样本，每一行代表一个特征（像素）。

  3. 计算协方差矩阵： 对数据矩阵进行协方差计算，得到一个协方差矩阵。协方差矩阵描述了不同特征之间的相关性。

  4. 特征值分解： 对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。特征向量代表了原始数据在新坐标系中的投影方向，而特征值表示数据在对应特征向量方向上的方差。

  5. 选择主成分： 根据特征值的大小，选择最大的几个特征值对应的特征向量作为主成分。主成分对应的特征向量表示了数据中最重要的方向。

  6. 降维： 将原始数据矩阵与选取的主成分特征向量相乘，得到降维后的数据矩阵。降维后的数据矩阵将保留了最重要的特征，同时减少了数据的维度。

  7. 重构： 将降维后的数据矩阵与选取的主成分特征向量的转置相乘，得到重构后的数据矩阵。重构后的数据矩阵可以近似地还原原始数据。

  8. 逆归一化： 将重构后的数据矩阵进行逆归一化，将像素值恢复到原始范围。

通过选择合适的主成分数量，可以在保留较高图像质量的同时实现图像的压缩。通常，选择的主成分数量越少，压缩比例越高，但图像质量也会相应降低。

需要注意的是，PCA压缩是有损压缩，因为压缩后的图像无法完全恢复为原始图像。压缩比例和图像质量之间存在着权衡。

具体代码如下:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from PIL import Image

# 读取图片
imag = plt.imread('butterfly.bmp')

image_array = np.array(imag)
# 将图像重塑为二维矩阵
reshaped_array = imag.reshape(-1, 437)

# 误差
errors=[]

for n_components in range(437, 0, -25):
    # 创建PCA对象，指定要保留的主成分数量
    pca = PCA(n_components=n_components)

    # 执行PCA降维
    compressed_array = pca.fit_transform(reshaped_array)

    # 重构压缩后的数据
    reconstructed_array = pca.inverse_transform(compressed_array)

    # 将数据形状转换回图像尺寸
    reconstructed_image_array = reconstructed_array.reshape(imag.shape)


    # 将重构的数据转换回图像
    reconstructed_image = reconstructed_image_array.astype(np.uint8)

    reconstruction_error = np.mean(np.square(reconstructed_image - image_array))
    errors.append(reconstruction_error)

    # 图片展示，需要则打开
    # plt.imshow(reconstructed_image)
    # plt.show()

plt.plot(range(437, 0, -25),errors)
plt.xlabel('保存的维数',fontproperties='SimHei')
plt.ylabel('均方误差',fontproperties='SimHei')
plt.show()

得到的均方误差关于保存的维数折线关系图：

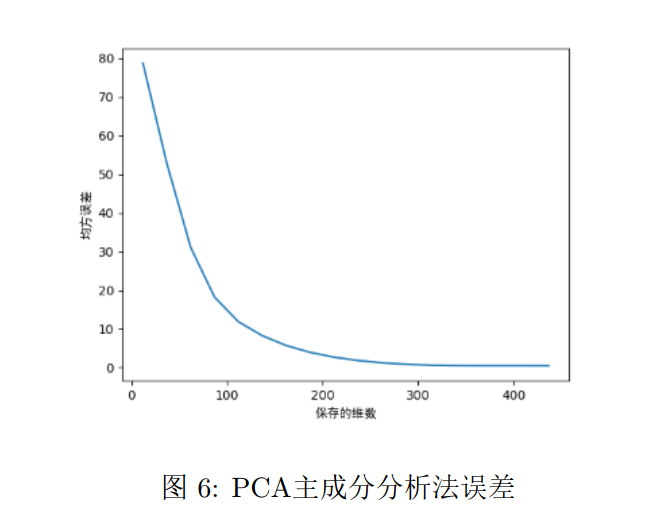
Alt text
Alt text

同时展示压缩后图片：
Alt text

总结

从图像压缩上对比两种算法，SVD只能处理灰度图，如果想要处理彩色图片，可能需要对三个通道分别处理。
而PCA主成分分析法则可以直接通过将三维张量reshape成二维矩阵的方式进行压缩，最后再转化为三维张量
（可能不同通道之间在算法进行时没有进行相互的影响？）。
而误差上较为类似，均是在去除大量低奇异值的或成分时候造成较小的误差。

而从数学上来讲，PCA 是一种基于协方差矩阵的线性降维方法，SVD 是一种矩阵分解方法。而且SVD中的右奇异值矩阵V
就是PCA主成分的方向，所以当数据量很大的时候可以通过求SVD分解得到有奇异值矩阵V作为PCA的主成分，

默认页脚
Copyright © 2025 Lzy